Dans la base de Frenet la vitesse s'écrit :
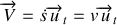
Le vecteur l'accélération s'obtient en dérivant par rapport au temps le vecteur vitesse :
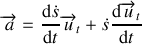
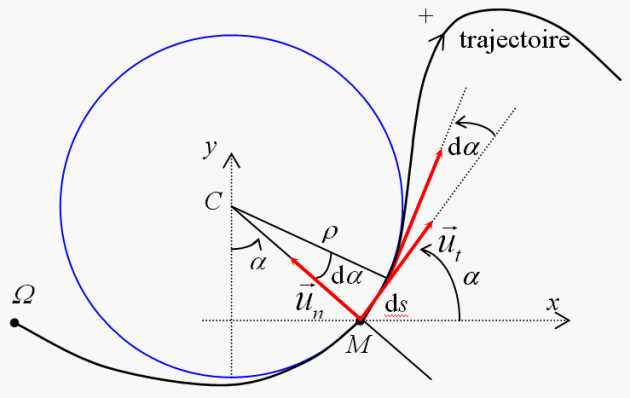
Figure 13 : Base de Frenet et déplacement
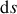élémentaire
À un instant
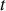, au point
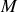de la trajectoire, le vecteur de base
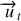fait un angle
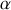avec la direction de l'axe des
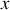(voir figure 13). À l'instant
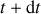, ce vecteur tourne d'un angle
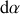. La dérivée, par rapport au temps, de ce vecteur unitaire est donc donnée par (voir règle de dérivation par rapport au temps d'un vecteur tournant de norme constante) :
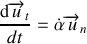
Avec
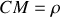, le rayon du cercle osculateur tangent à la courbe au point
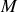, on a :
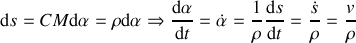
Finalement :
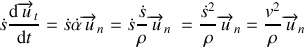
L'expression du vecteur accélération dans la base de Frenet est :
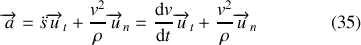
Remarque :
On pourra vérifier que ce résultat est toujours vrai quelle que soit la concavité de la trajectoire.
La composante normale de l'accélération
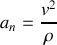est toujours positive : elle est toujours tournée vers le centre de courbure de la trajectoire au point considéré. Elle indique que la direction du vecteur vitesse change et est d'autant plus important que le rayon de courbure est faible (virage serré). Si le mouvement est rectiligne (rayon de courbure infini) ce terme est nul.
La composante tangentielle de l'accélération
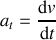, indique si la valeur de la vitesse change. Si le mouvement est uniforme ce terme est nul.
